Fisica al Desnudo

sábado, 15 de octubre de 2011

Fisica Tercer Periodo

moviemiento en dos dimensiones
En general e1 movimiento de los objetos verdaderos se realiza en el espacio
real tridimensional. E1 movimiento de una partícula que se realiza en un plano
es un movimiento en dos dimensiones, si el movimiento se realiza en el espacio, se produce en tres dimensiones. En este capítulo se estudia la cinemática
de una partícula que se mueve sobre un plano. Ejemplos de un movimiento en
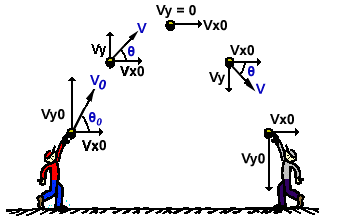
dos dimensiones son el de un cuerpo que se lanza al aire, tal como una pelota,
un disco girando, el salto de un canguro, el movimiento de planetas y satélites,
etc. El movimiento de los objetos que giran en una órbita cuya trayectoria es
una circunferencia, se conoce como movimiento circunferencial; es un caso de
movimiento en dos dimensiones, que también es estudiado en este capítulo. El
vuelo de una mosca, el de un avión o el movimiento de las nubes se produce
en tres dimensiones.
3.1 DESCRIPCIÓN DEL MOVIMIENTO EN DOS DIMENSIONES.
Continuamos restringiendo el estudio del movimiento al caso de una partícula
que se mueve con aceleración constante, es decir que su magnitud y dirección no cambian durante el movimiento. E1 vector posición de una partícula
que se mueve en el plano xy es una función del tiempo, se escribe como:
r (t) = x(t)iˆ + y(t) ˆj
r
Por definición, la velocidad de la partícula en movimiento en el plano xy es, el
cambio de posición en el transcurso del tiempo y se puede determinar por:
j v i v j
dt
dy
i
dt
dx
dt
dr
v
x y
= = ˆ + ˆ = ˆ + ˆ
r
r
es decir,
j
ˆ
i v ( t )
ˆ
v( t ) v ( t ) = x
+ y
rCap. 3 Movimiento en dos Dimensiones
76
donde vx y vy son las componentes de la velocidad en la dirección x e y. Si la
aceleración es constante, sus componentes ax en la dirección x, y ay en la dirección y, también lo son. Aplicando las ecuaciones cinemáticas de la velocidad deducidas para el movimiento en una dimensión, independientemente en
cada dirección x e y, para una partícula que en el instante inicial to se mueve
con velocidad inicial v v i v j
o ox oy
ˆ ˆ
r r r
= + se obtienen las componentes de la
velocidad en función del tiempo:
v v a ( t t )
v v a ( t t )
y oy y o
x ox x o
= + −
= + −
reemplazando en la expresión de v( t )
r
, se obtiene la velocidad en cualquier
instante t:
[ ] [ ]
( ) ( ˆ ˆ) ( ˆ ˆ)( )
( ) ( ) ˆ ( ) ˆ
ox oy x y o
ox x o oy y o
v t v i v j a i a j t t
v t v a t t i v a t t j
= + + + −
= + − + + −
r
r
v( t ) v a( t t ) = o
+ − o
r r r
(3.1)
De manera similar reemplazando las expresiones de la posición en función del
tiempo en cada dirección x e y, para una partícula que en el instante inicial to
se encuentra en la posición inicial r x i y j
o o o
= ˆ + ˆ
r
se obtiene la posición r( t )
r
de la partícula, en cualquier instante t:
2
( )
2
1
( )
o ox o x o
x = x + v t − t + a t − tCap. 3 Movimiento en dos Dimensiones
77
2
( )
2
1
( )
o oy o y o
y = y + v t − t + a t − t
2
( )
2
1
( ) ( )
o o o o
r t = r + v t − t + a t − t
r r r r
(3.2)
Se concluye que el movimiento bidimensional con aceleración constante es
equivalente a dos movimientos independientes en las direcciones x e y con
aceleraciones constantes ax y ay. A esta propiedad se le llama principio de independencia del movimiento.

Movimiento Parabolico

Cuando un objeto es lanzado con cierta inclinación respecto a la horizontal y bajo la acción solamente de la fuerza gravitatoria su trayectoria se mantiene en el plano vertical y es parabólica.

Nótese que estamos solamente tratando el caso partícular en que factores como la resistencia del aire, la rotación de la Tierra, etc., no introducen afectaciones apreciables. Vamos a considerar también que durante todo el recorrido la aceleración debido a la gravedad ( g ) permanece constante y que el movimiento es sólo de traslación.

Para facilitar el estudio del movimiento de un proyectil, frecuentemente este se descompone en las direcciones horizontal y vertical. En la dirección horizontal el movimiento del proyectil es rectilíneo y uniforme ya que en esa dirección la acción de la gravedad es nula y consecuente, la aceleración también lo es. En la dirección vertical, sobre el proyectil actúa la fuerza de gravedad que hace que el movimiento sea rectilíneo uniformemente acelerado, con aceleración constante.

Sea un proyectil lanzado desde un cañón. Si elegimos un sistema de referencia de modo que la dirección Y sea vertical y positiva hacia arriba, a _y = - g y a _x = 0. Además suponga que el instante t = 0, el proyectil deja de origen (X _i= Y _i = 0) con una velocidad V_i.

Si Vi hace un ángulo qi con la horizontal, a partir de las definiciones de las funciones sen y cos se obtiene:

V_xi = V_i cos θ
Vyi = V_i sen θ_i

Como el movimiento de proyectiles es bi-dimencional, donde a_x = 0 y a_y = -g, o sea con aceleración constante, obtenemos las componentes de la velocidad y las coordenadas del proyectil en cualquier instante t, con ayuda de las ecuaciones ya utilizadas para el M.R.U.A. Expresando estas en función de las proyecciones tenemos:

X = V_xit = Vi cos θ_i t
y = V_yi t + ½ at²
V_yf = V_yi + at
2ay = V_yf² - V_yi²

Si un proyectil es lanzado horizontalmente desde cierta altura inicial, el movimiento es semi-parabólico.

Las ecuaciones del movimiento considerando Vyi = 0 serían:

X = V_xi t

y = y_o - ½ gt²

Recomendamos la realización de la práctica virtual Movimiento bajo la aceleración constante de la gravedad, donde se puede estudiar tanto el movimiento parabólico como el semi-parabólico.

Combinando las ecuaciones arriba explicadas para el movimiento parabólico podemos algunas obtener ecuaciones útiles:

- Altura máxima que alcanza un proyectil:

- Tiempo de vuelo del proyectil:

- Alcance del proyectil :

Atendiendo a esta última ecuación, invitamos al lector a demostrar que para una velocidad dada el máximo alcance se logra con una inclinacion de 45o respecto a la horizontal.

Cinematica

La Cinemática (del griego κινεω, kineo, movimiento) es la rama de la mecánica clásica que estudia las leyes del movimiento de los cuerpos sin tener en cuenta las causas que lo producen, limitándose, esencialmente, al estudio de la trayectoria en función del tiempo.

En la Cinemática se utiliza un sistema de coordenadas para describir las trayectorias, denominado sistema de referencia. La velocidad es el ritmo con que cambia la posición un cuerpo. La aceleración es el ritmo con que cambia su velocidad. La velocidad y la aceleración son las dos principales cantidades que describen cómo cambia su posición en función del tiempo.

Cinemática clásica. Fundamentos
La Cinemática trata del estudio del movimiento de los cuerpos en general, y, en particular, el caso simplificado del movimiento de un punto material. Para sistemas de muchas partículas, tales como los fluidos, las leyes de movimiento se estudian en la mecánica de fluidos. El movimiento trazado por una partícula lo mide un observador respecto a un sistema de referencia. Desde el punto de vista matemático, la Cinemática expresa cómo varían las coordenadas de posición de la partícula (o partículas) en función del tiempo. La función que describe la trayectoria recorrida por el cuerpo (o partícula) depende de la velocidad (la rapidez con la que cambia de posición un móvil) y de la aceleración (variación de la velocidad respecto del tiempo).
El movimiento de una partícula (o cuerpo rígido) se puede describir según los valores de velocidad y aceleración, que son magnitudes vectoriales.
Si la aceleración es nula, da lugar a un movimiento rectilíneo uniforme y la velocidad permanece constante a lo largo del tiempo.

Si la aceleración es constante con igual dirección que la velocidad, da lugar al movimiento rectilíneo uniformemente acelerado y la velocidad variará a lo largo del tiempo.

Si la aceleración es constante con dirección perpendicular a la velocidad, da lugar al movimiento circular uniforme, donde el módulo de la velocidad es constante, cambiando su dirección con el tiempo.

Cuando la aceleración es constante y está en el mismo plano que la velocidad y la trayectoria, tenemos el caso del movimiento parabólico, donde la componente de la velocidad en la dirección de la aceleración se comporta como un movimiento rectilíneo uniformemente acelerado, y la componente perpendicular se comporta como un movimiento rectilíneo uniforme, generándose una trayectoria parabólica al componer ambas.

Cuando la aceleración es constante pero no está en el mismo plano que la velocidad y la trayectoria, se observa el efecto de Coriolis.

En el movimiento armónico simple se tiene un movimiento periódico de vaivén, como el del péndulo, en el cual un cuerpo oscila a un lado y a otro desde la posición de equilibrio en una dirección determinada y en intervalos iguales de tiempo. La aceleración y la velocidad son funciones, en este caso, sinusoidales del tiempo.

Al considerar el movimiento de traslación de un cuerpo extenso, en el caso de ser rígido, conociendo como se mueve una de las partículas, se deduce como se mueven las demás. Así basta describir el movimiento de una partícula puntual tal como el centro de masa del cuerpo para especificar el movimiento de todo el cuerpo. En la descripción del movimiento de rotación hay que considerar el eje de rotación respecto del cual rota el cuerpo y la distribución de partículas respecto al eje de giro. El estudio del movimiento de rotación de un sólido rígido suele incluirse en la temática de la mecánica del sólido rígido por ser más complicado. Un movimiento interesante es el de una peonza, que al girar puede tener un movimiento de precesión y de nutación
Cuando un cuerpo posee varios movimientos simultáneamente, tal como uno de traslación y otro de rotación, se puede estudiar cada uno por separado en el sistema de referencia que sea apropiado para cada uno, y luego, superponer los movimientos.

Fuerzas

Fuerzas

En física, la fuerza es una magnitud física que mide la intensidad del intercambio de momento lineal entre dos partículas o sistemas de partículas (en lenguaje de la física de partículas se habla de interacción). Según una definición clásica, fuerza es todo agente capaz de modificar la cantidad de movimiento o la forma de los cuerpos materiales. No debe confundirse con los conceptos de esfuerzo o de energía.

En el Sistema Internacional de Unidades, la fuerza se mide en newtons (N).

a fuerza es una modelización matemática de intensidad de las interacciones, junto con la energía. Así por ejemplo la fuerza gravitacional es la atracción entre los cuerpos que tienen masa, el peso es la atracción que la Tierra ejerce sobre los objetos en las cercanías de su superficie, la fuerza elástica es el empuje o tirantez que ejerce un resorte comprimido o estirado respectivamente, etc. En física hay dos tipos de ecuaciones de fuerza: las ecuaciones "causales" donde se especifica el origen de la atracción o repulsión: por ejemplo la ley de la gravitación universal de Newton o la ley de Coulomb y las ecuaciones de los efectos (la cual es fundamentalmente la segunda ley de Newton).

La fuerza es una magnitud física de carácter vectorial capaz de deformar los cuerpos (efecto estático), modificar su velocidad o vencer su inercia y ponerlos en movimiento si estaban inmóviles (efecto dinámico). En este sentido la fuerza puede definirse como toda acción o influencia capaz de modificar el estado de movimiento o de reposo de un cuerpo (imprimiéndole una aceleración que modifica el módulo o la dirección de su velocidad) o bien de deformarlo.

Comúnmente nos referimos a la fuerza aplicada sobre un objeto sin tener en cuenta al otro objeto u objetos con los que está interactuando y que experimentarán, a su vez, otras fuerzas. Actualmente, cabe definir la fuerza como un ente físico-matemático, de carácter vectorial, asociado con la interacción del cuerpo con otros cuerpos que constituyen su entorno.

Fisicasegundo Periodo

Movimiento Bidimensional
Movimiento en una y dos dimensiones: Cinemática. Movimiento rectilíneo uniforme y uniformemente acelerado. Posición, velocidad, aceleración. Tiro parabólico, caída libre. Circular
Movimiento dos dimensiones
Cuando pateas un balón, el balón hace un movimiento en dos dimensiones llamado tiro parabólico.
Se le llama en dos dimensiones, porque la posición de la partícula en cada instante, se puede representar por dos coordenadas, respecto a unos ejes de referencia.
El movimiento en 2 dimensiones es cuando la partícula se mueve tanto horizontal como verticalmente (por así decirlo).
El movimiento de una partícula en dos dimensiones es la trayectoria de la partícula en un plano (vertical, horizontal, o en cualquier otra dirección del plano).Las variables a las que está sometida la partícula son dos y por eso se le denomina movimiento en dos dimensiones.
MOVIMIENTOS RECTILÍNEOS CON ACELERACIÓN CTE.
Ecuación de la velocidad: v - vo = a (t - to) __> v = vo + at

lanzamiento de proyectil (parabolico)

Si Vi hace un ángulo qi con la horizontal, a partir de las definiciones de las funciones sen y cos se obtiene:

V_xi = V_i cos θ
Vyi = V_i sen θ_i

X = V_xit = Vi cos θ_i t
y = V_yi t + ½ at²
V_yf = V_yi + at
2ay = V_yf² - V_yi²

Si un proyectil es lanzado horizontalmente desde cierta altura inicial, el movimiento es semi-parabólico.

Las ecuaciones del movimiento considerando Vyi = 0 serían:

X = V_xi t

y = y_o - ½ gt²

Recomendamos la realización de la práctica virtual Movimiento bajo la aceleración constante de la gravedad, donde se puede estudiar tanto el movimiento parabólico como el semi-parabólico.

Combinando las ecuaciones arriba explicadas para el movimiento parabólico podemos algunas obtener ecuaciones útiles:

- Altura máxima que alcanza un proyectil:

- Tiempo de vuelo del proyectil:

- Alcance del proyectil :

Atendiendo a esta última ecuación, invitamos al lector a demostrar que para una velocidad dada el máximo alcance se logra con una inclinacion de 45o respecto a la horizontal.

Caida Libre

En física, se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las caídas reales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo es frecuente también referirse coloquialmente a éstas como caídas libres, aunque los efectos de la viscosidad del medio no sean por lo general despreciables.

El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción desaceleradora de la gravedad, como un disparo vertical; o a satélites no propulsados en órbita alrededor de la Tierra, como la propia Luna. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.

Ejemplos de caída libre deportiva los encontramos en actividades basadas en dejarse caer una persona a través de la atmósfera sinsustentación alar ni de paracaídas durante un cierto trayecto.¹ ²

Por la segunda ley de Newton, la fuerza $\mathbf{F}$ que actúa sobre un cuerpo es igual al producto de su masa $m\,$ por la aceleración que adquiere. En caída libre sólo intervienen el peso $\mathbf{P}$ (vertical, hacia abajo) y el rozamiento aerodinámico $\mathbf{f}(v)$ en la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo gravitatorio aproximadamente constante, la ecuación del movimiento de caída libre es:

$\mathbf{F} = \mathbf{P}+\mathbf{f} = -mg {\mathbf{j}} - f\frac{\mathbf{v}}{v} = m\frac{d\mathbf{v}}{dt}$

La aceleración de la gravedad $g\,$ lleva signo negativo porque se toma el eje vertical como positivo hacia arriba.

Trayectoria en caída libre

[editar]Caída libre totalmente vertical

El movimiento del cuerpo en caída libre es vertical con velocidad creciente (aproximadamente movimiento uniformemente acelerado con aceleración g) (aproximadamente porque la aceleración aumenta cuando el objeto disminuye en altura, en la mayoría de los casos la variación es despreciable). La ecuación de movimiento se puede escribir en términos la altura y:

(1) $-mg + f = ma_y \,$

donde:

$a_y, v_y\;$ , son la aceleración y la velocidad verticales.

$f\;$ , es la fuerza de rozamiento fluidodinámico (que aumenta con la velocidad).

Si, en primera aproximación, se desprecia la fuerza de rozamiento, cosa que puede hacerse para caídas desde pequeñas alturas de cuerpos relativamente compactos, en las que se alcanzan velocidades moderadas, la solución de la ecuación diferencial (1) para las velocidades y la altura vienen dada por:

$\begin{matrix} v_y(t)= v_0 - gt \\ y(t) = h_0 + v_0t -\frac{1}{2}gt^2 \end{matrix}$

donde v₀ es la velocidad inicial, para una caída desde el reposo v₀ = 0 y h₀ es la altura inicial de caída.

Para grandes alturas u objetos de gran superficie (una pluma, un paracaídas) es necesario tener en cuenta la resistencia fluidodinámica que suele ser modelizada como una fuerza proporcional a la velocidad, siendo la constante de proporcionalidad el llamado rozamiento aerodinámico k_w:

(2) $-mg - k_wv_y = ma_y \,$

En este caso la variación con el tiempo de la velocidad y el espacio recorrido vienen dados por la solución de la ecuación diferencial (2):

$\begin{cases} v_y = v_0e^{-k_wt/m} + \cfrac{mg}{k_w}(e^{-k_wt/m}-1) \\ y = h_0 - \cfrac{mgt}{k_w}+m\left(\cfrac{mg+k_wv_0}{k_w^2}\right)(e^{-k_wt/m}-1) \end{cases}$

Nótese que en este caso existe una velocidad límite dada por el rozamiento aerodinámico y la masa del cuerpo que cae:

$v_\infty = \lim_{t\to \infty} v_y(t) = -\frac{mg}{k_w}$

Un análisis más cuidadoso de la fricción de un fluido revelaría que a grandes velocidades el flujo alrededor de un objeto no puede considerarse laminar, sinoturbulento y se producen remolinos alrededor del objeto que cae de tal manera que la fuerza de fricción se vuelve proporcional al cuadrado de la velocidad:

(3) $ma_y = m\frac{d^2y}{dt^2} = -mg - \epsilon\frac{C_d}{2}\rho A_tv_y^2$

Donde:

$C_d\;$ , es el coeficiente aerodinámico de resistencia al avance, que sólo depende de la forma del cuerpo.

$A_t\;$ , es el área transversal a la dirección del movimiento.

$\rho\;$ , es la densidad del fluido.

$\epsilon = sgn(v_y)\;$ , es el signo de la velocidad.

La velocidad límite puede calcularse fácilmente poniendo igual a cero la aceleración en la ecuación (3):

$v_\infty = \sqrt{\frac{2mg}{C_d\rho A_t}}$

La solución analítica de la ecuación diferencial (3) depende del signo relativo de la fuerza de rozamiento y el peso por lo que la solución analítica es diferente para un cuerpo que sube o para uno que cae. La solución de velocidades para ambos casos es:

$\begin{cases} v_y(t)= \sqrt{\cfrac{g}{\alpha}} \tan\left(-t\sqrt{{\alpha}{g}} +\arctan\left(v_0\sqrt{\cfrac{\alpha}{g}}\right) \right) & v_y(t) > 0\\ v_y(t)= \sqrt{\cfrac{g}{\alpha}} \tanh\left(-t\sqrt{{\alpha}{g}} -\mbox{arctanh}\left(v_0\sqrt{\cfrac{\alpha}{g}}\right) \right) & v_y(t) \le 0 \end{cases}$

Donde: $\alpha = C_d\rho A_t/2m\;$ .

Si se integran las ecuaciones anteriores para el caso de caída libre desde una altura

h 0

y velocidad inicial nula y para el caso de lanzamiento vertical desde una altura nula con una velocidad inicial

v 0

se obtienen los siguientes resultados para la altura del cuerpo:

Caída libre (

v 0 = 0

y (0) = h 0

$y(t)=h_0-\cfrac{1}{{\alpha}}\ln\left[\cosh\left(-t\sqrt{{\alpha}{g}}\right) \right]$

El tiempo transcurrido en la caída desde la altura

y = h 0

hasta la altura

y = 0

puede obtenerse al reordenar la ecuación anterior:

$t(0)-t(h_0)=\cfrac{1}{\sqrt{{\alpha}{g}}}\mbox{arccosh}\left(e^{{\alpha}h_0}\right)$

Lanzamiento vertical (

v 0 = v 0

y (0) = 0

$y(t)=\cfrac{1}{{\alpha}}\ln\left[\cfrac{\cos\left[-t\sqrt{{\alpha}{g}}+\arctan\left(v_0\sqrt{\cfrac{\alpha}{g}}\right)\right]}{\cos\left[\mbox{arctan}\left(v_0\sqrt{\cfrac{\alpha}{g}}\right)\right]} \right]$

Si la altura

h 0

es aquella en que la velocidad vertical se hace cero, entonces el tiempo transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura

h 0

puede calcularse como:

$t(h_0)-t(0)=\cfrac{1}{\sqrt{{\alpha}g}}\mbox{arctan}\left(v_0\sqrt{\cfrac{\alpha}{g}}\right)=\cfrac{1}{\sqrt{{\alpha}g}}\mbox{arccos}\left(e^{-{\alpha}h_0}\right)$

Se puede demostrar que el tiempo que tarda un cuerpo en caer desde una altura

h 0

hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en alcanzar la alura máxima de

h 0

si es lanzado desde el suelo. Para ello basta con probar la desigualdad siguiente:

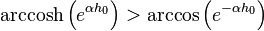
$\mbox{arccosh}\left(e^{{\alpha}h_0}\right)>\mbox{arccos}\left(e^{-{\alpha}h_0}\right)$

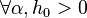
$\forall \alpha, h_0 > 0$

sabiendo que $\mbox{arccosh}\left(e^{{\alpha}h_0}\right)\in\left[1,+\infty\right)$ y que $\mbox{arccos}\left(e^{-{\alpha}h_0}\right)\in\left[0,\cfrac{\pi}{2}\right]$